Оценка S в одной и той же около среднего их значения, вычисляемая по 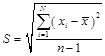 (9.6), где xi — результат i–го единичного измерения,
(9.6), где xi — результат i–го единичного измерения, 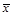 — среднее арифметическое значение измеряемой величины из n единичных результатов.
— среднее арифметическое значение измеряемой величины из n единичных результатов.
— На практике широко распространен среднее квадратическое отклонение — (СКО). Под отклонением в с формулой (9.6) понимают отклонение единичных результатов в ряду измерений от их среднего арифметического значения. В , как отмечено в 9.1, это отклонение называется . Если в введены на действие , то отклонения представляют собой . Поэтому с точки зрения упорядочения совокупности терминов, родовым среди которых является термин «погрешность измерения», целесообразно применять термин «средняя квадратическая погрешность». При обработке ряда результатов измерений, свободных от систематических погрешностей, СКП и СКО являются одинаковой оценкой рассеяния результатов единичных измерений.
[из 9.14 РМГ 29–99]